What is a linked list? (in C)

A linked list is either:

• null, or
• a node, containing a value and a pointer to a linked list.

Because the definition of a list refers to its own name inside its definition, it is a recursive data structure.

It is sometimes easier to think about things graphically, so here is a way to visualize the definition above.

The value null is represented by the symbol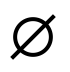

A node contains storage for a value and a pointer (to a list) and is represented by the symbol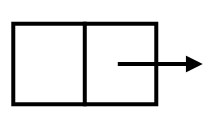

Graphically, a list is either:

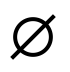• , or
• 

Here is an example, graphically, of a list that contains three elements:

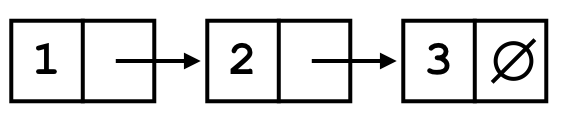
When we print this list in order, we should get:

1
2
3

Notice that a node must always point at a list. The following is not a valid list, because one of pointers points at nothing:

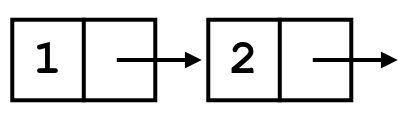
Parts of a list

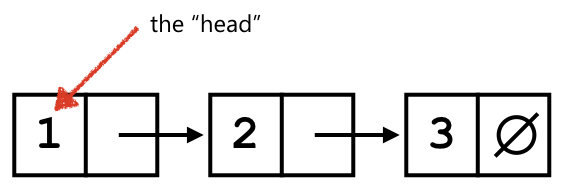
The parts of a list have names: the head and the tail.

Suppose that you have a list node whose value is of type T (Note that I use the generic type T here as a placeholder; C does not actually have generic types like Java, but there’s no reason that you cannot build a list for an arbitrary type in C, so I use T to refer to whatever type you might want to use, like int or char *).

Conventionally, the head of the list is the value at the beginning or front of the list.

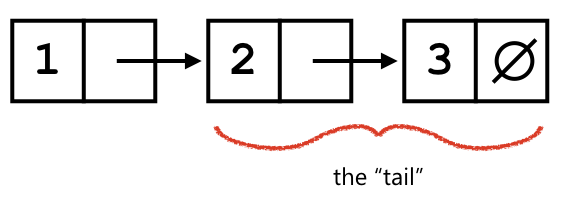
The tail is the entire list after the node that stores the head.

This definition seems a tad inelegant when phrased this way, so here’s another way of thinking about it. The head is the value stored in the head field of a node; the tail is the value stored in the tail field of a node.

Since the tail field is always a pointer to a list, it is actually equivalent to the remainder of the list.

Fundamental list operations

Since we name the parts of a list, it is often convenient for us to have list operations that return those parts.

The head function returns the head of the list (of some type T):

T head(listnode *lst);

The tail function returns the tail of the list:

listnode *tail(listnode *lst);

We also need a way to add data to a list. There are two ways to add data. The first is to prepend data. The prepend function adds a node to the front of the list and returns a pointer to the new head:

listnode *prepend(T data, listnode *lst);

So the list:

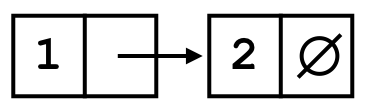
prepended with the element containing 3 becomes:

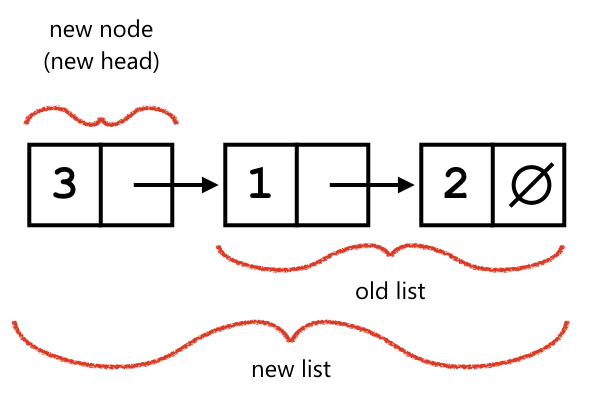
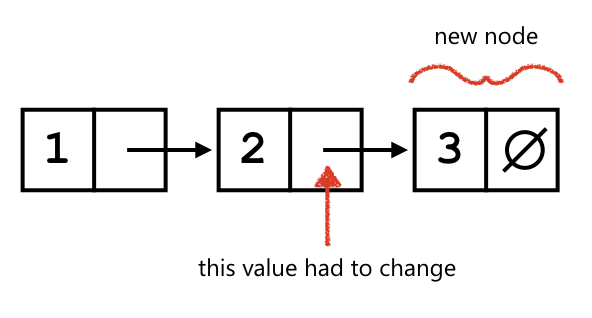
The other way to add data is to append data, which mutates the last element:

listnode *append(T data);

So the list:

appended with the element containing 3 beccomes:

Asymptotic complexity

Newcomers to linked lists are often surprised that computer scientists overwhelmingly favor list prepend over list append. Why? Prepending is much faster. Consider how many traversal operations need to be performed to prepend:

1. Set lst equal to the list.
2. Create a new listnode and point it at lst.

That’s 2 steps. O(1) operations.

Consider how many traversal operations need to be performed to append:

1. Set lst equal to the list.
2. Read the tail field of listnode lst
3. If the tail is null, create a new listnode and point lst’s tail pointer at the new node. Otherwise, set the lst to tail and go to step 2.

That’s many more steps than prepend, depending on the length of the list. O(n) steps, to be precise.

If we can accomplish something in O(1) steps vs O(n) steps, we will generally favor the O(1) version unless there is a compelling reason not to. You might notice that, using prepend, our list ends up backward. That is not usually a compelling reason. Why? Because we can reverse a list in O(n). While that doesn’t sound like a big win for add a single element, when adding n elements, the savings are huge.

Prepending and reversing a list of n elements: O(1) * n + O(n) = O(n)

Appending a list of n elements: O(n) * n = O(n^2) (we can make this bound a tad tighter, but asymptotically, it is the same).

Another reason to favor prepending is that, when adding a new node, the original list is totally unchanged. All of the “changes” to the list are confined to the new data. Thus, lists are easy to build and work with in a functional way, because functional programming requires that data structures be immutable. We will talk in depth about these properties when we start our section on the ML programming language.