Grammars and Parse Trees

(Excerpted from Mitchell’s “Concepts in Programming Languages”, pp. 52–57)

We use grammars to describe various languages in this book. Although we usually are not too concerned about the pragmatics of parsing, we take a brief look in this subsection at the problem of producing a parse tree from a sequence of tokens.

Grammars

Grammars provide a convenient method for defining infinite sets of expressions. In addition, the structure imposed by a grammar gives us a systematic way of processing expressions.

A grammar consists of a start symbol, a set of nonterminals, a set of terminals, and a set of productions. The nonterminals are symbols that are used to write out the grammar, and the terminals are symbols that appear in the language generated by the grammar. In books on automata theory and related subjects, the productions of a grammar are written in the form s → tu, with an arrow, meaning that in a string containing the symbol s, we can replace s with the symbols tu. However, here we use a more compact notation, commonly referred to as BNF.

The main ideas are illustrated by example. A simple language of numeric expressions is defined by the following grammar:

e ::= n | e+e | e-e
n ::= d | nd
d ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

where e is the start symbol, symbols e, n, and d are nonterminals, and 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, and - are the terminals. The language defined by this grammar consists of all the sequences of terminals that we can produce by starting with the start symbol e and by replacing nonterminals according to the preceding productions. For example, the first preceding production means that we can replace an occurrence of e with the symbol n, the three symbols e+e, or the three symbols e-e. The process can be repeated with any of the preceding three lines.

Some expressions in the language given by this grammar are

0, 1 + 3 + 5, 2 + 4 – 6 - 8

Sequences of symbols that contain nonterminals, such as

e, e+e, e+6-e

are not expressions in the language given by the grammar. The purpose of nonterminals is to keep track of the form of an expression as it is being formed. All nonterminals must be replaced with terminals to produce a well-formed expression of the language.

Derivations

A sequence of replacement steps resulting in a string of terminals is called a derivation.

Here are two derivations in this grammar, the first given in full and the second with a few missing steps that can be filled in by the reader (be sure you understand how!):

e → n → nd → dd → 2d → 25

e → e-e → e-e+e → … → n-n+n → … → 10-15+12

Parse Trees and Ambiguity

It is often convenient to represent a derivation by a tree. This tree, called the parse tree of a derivation, or derivation tree, is constructed with the start symbol as the root of the tree. If a step in the derivation is to replace s with x₁ , … ,x_n , then the children of s in the tree will be nodes labeled x₁ , … ,x_n. The parse tree for the derivation of 10-15+12 in the preceding subsection has some useful structure. Specifically, because the first step yields e-e, the parse tree has the form

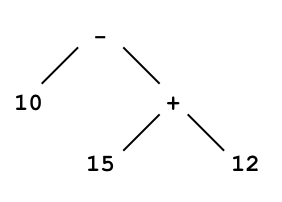
where we have contracted the subtrees for each two-digit number to a single node. This tree is different from

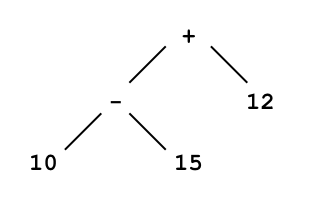
which is another parse tree for the same expression. An important fact about parse trees is that each corresponds to a unique parenthesization of the expression. Specifically, the first tree corresponds to 10-(15+12) whereas the second corresponds to (10-15)+12. As this example illustrates, the value of an expression may depend on how it is parsed or parenthesized.

A grammar is ambiguous if some expression has more than one parse tree. If every expression has at most one parse tree, the grammar is unambiguous.

Example 4.1

There is an interesting ambiguity involving if-then-else. This can be illustrated by the following simple grammar:

s ::= v := e | s;s | if b then s | if b then s else s
v ::= x | y | z
e ::= v | 0 | 1 | 2 | 3 | 4
b ::= e=e

where s is the start symbol, s, v, e, and b are nonterminals, and the other symbols are terminals. The letters s, v, e, and b stand for statement, variable, expression, and Boolean test, respectively. We call the expressions of the language generated by this grammar statements.

Here is an example of a well-formed statement and one of its parse trees:

x := 1; y := 2; if x=y then y := 3

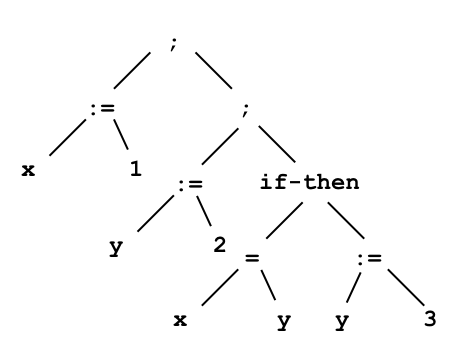
This statement also has another parse tree, which we obtain by putting two assignments to the left of the root and the if-then statement to the right. However, the difference between these two parse trees will not affect the behavior of code generated by an ordinary compiler. The reason is that is normally compiled to the code for s₁ followed by the code for s₂. As a result, the same code would be generated whether we consider s₁;s₂:s₃ as (s₁;s₂);s₃ or s₁;(s₂;s₃).

A more complicated situation arises when if-then is combined with if-then-else in the following way:

if b1 then if b2 then s1 else s2

What should happen if b₁ is true and b₂ is false? Should s₂ be executed or not? As you can see, this depends on how the statement is parsed. A grammar that allows this combination of conditionals is ambiguous, with two possible meanings for statements of this form.

Parsing and Precedence

Parsing is the process of constructing parse trees for sequences of symbols. Suppose we define a language L by writing out a grammar G. Then, given a sequence of symbols s, we would like to determine if s is in the language L. If so, then we would like to compile or interpret s, and for this purpose we would like to find a parse tree for s. An algorithm that decides whether s is in L, and constructs a parse tree if it is, is called a parsing algorithm for G.

There are many methods for building parsing algorithms from grammars. Many of these work for only particular forms of grammars. Because parsing is an important part of compiling programming languages, parsing is usually covered in courses and textbooks on compilers. For most programming languages you might consider, it is either straightforward to parse the language or there are some changes in syntax that do not change the structure of the language very much but make it possible to parse the language efficiently.

Two issues we consider briefly are the syntactic conventions of precedence and right or left associativity. These are illustrated briefly in the following example.

Example 4.2

A programming language designer might decide that expressions should include addition, subtraction, and multiplication and write the following grammar:

e ::= 0 | 1 | e+e | e-e | e*e

This grammar is ambiguous, as many expressions have more than one parse tree. For expressions such as 1-1+1, the value of the expression will depend on the way it is parsed. One solution to this problem is to require complete parenthesization. In other words, we could change the grammar to

e ::= 0 | 1 | (e+e) | (e-e) | (e*e)

so that it is no longer ambiguous. However, as you know, it can be awkward to write a lot of parentheses. In addition, for many expressions, such as 1+2+3+4, the value of the expression does not depend on the way it is parsed. Therefore, it is unnecessarily cumbersome to require parentheses for every operation.

The standard solution to this problem is to adopt parsing conventions that specify a single parse tree for every expression. These are called precedence and associativity. For this specific grammar, a natural precedence convention is that multiplication has a higher precedence than addition (+) and subtraction (—). We incorporate precedence into parsing by treating an unparenthesized expression e op1 e ep2 e as if parentheses are inserted around the operator of higher precedence. With this rule in effect, the expression 5*4-3 will be parsed as if it were written as (5*4)-3. This coincides with the way that most of us would ordinarily think about the expression 5*4-3. Because there is no standard way that most readers would parse 1+1-1, we might give addition and subtraction equal precedence. In this case, a compiler could issue an error message requiring the programmer to parenthesize 1+1-1. Alternatively, an expression like this could be disambiguated by use of an additional convention.

Associativity comes into play when two operators of equal precedence appear next to each other. Under left associativity, an expression e op1 e op2 e would be parsed as (e op1 e) op2 e, if the two operators have equal precedence. If we adopted a right-associativity convention instead, e op1 e op2 e would be parsed as e op1 (e op2 e).

Expression	Precedence	Left Associativity	Right Associativity
5*4-3	(5*4)-3	no change	no change
1+1-1	no change	(1+1)-1	1+(1-1)
2+3-4*5+2	2+3-(4*5)+2	((2+3)-(4*5))+2	2+(3-((4*5))+2))